The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other. Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order. Each solution contains a distinct board configuration of the n-queens' placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space, respectively.
Example 1:
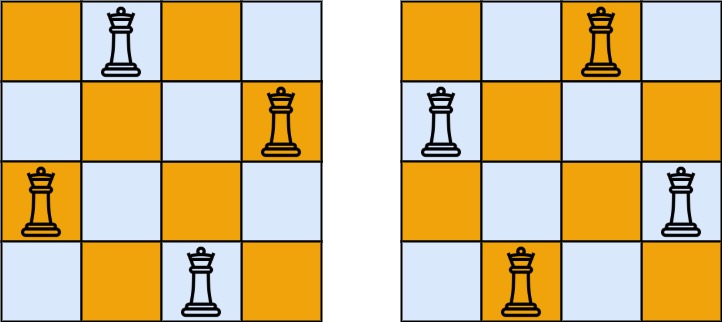Input: n = 4 Output: [[".Q..","…Q",“Q…”,"..Q."],["..Q.",“Q…”,"…Q",".Q.."]] Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2: Input: n = 1 Output: [[“Q”]]
Constraints:
1 <= n <= 9
- code brute force
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
res = []
def put_queue(board, row_start, col_start):
for i in range(n):
board[i][col_start] = "N" # Q makes it invalid
row, col = row_start, col_start
while 0 <= row + 1 < n and 0 <= col + 1 < n:
row, col = row + 1, col + 1
board[row][col] = "N"
row, col = row_start, col_start
while 0 <= row - 1 < n and 0 <= col - 1 < n:
row, col = row - 1, col - 1
board[row][col] = "N"
row, col = row_start, col_start
while 0 <= row + 1 < n and 0 <= col - 1 < n:
row, col = row + 1, col - 1
board[row][col] = "N"
row, col = row_start, col_start
while 0 <= row - 1 < n and 0 <= col + 1 < n:
row, col = row - 1, col + 1
board[row][col] = "N"
board[row_start][col_start] = "Q"
return board
def dfs(queue_row, board):
if queue_row == n:
for row in range(n):
for col in range(n):
if board[row][col] == "N":
board[row][col] = "."
res.append("".join(row) for row in board)
return
for col in range(n):
if board[queue_row][col] == ".":
old_board = copy.deepcopy(board)
new_board = put_queue(board, queue_row, col)
dfs(queue_row + 1, new_board)
board = copy.deepcopy(old_board)
board = [["." for j in range(n)] for i in range(n)]
dfs(0, board)
return res
- code
class Solution:
def solveNQueens(self, n):
# Making use of a helper function to get the
# solutions in the correct output format
def create_board(state):
board = []
for row in state:
board.append("".join(row))
return board
def backtrack(row, diagonals, anti_diagonals, cols, state):
# Base case - N queens have been placed
if row == n:
ans.append(create_board(state))
return
for col in range(n):
curr_diagonal = row - col
curr_anti_diagonal = row + col
# If the queen is not placeable
if (col in cols
or curr_diagonal in diagonals
or curr_anti_diagonal in anti_diagonals):
continue
# "Add" the queen to the board
cols.add(col)
diagonals.add(curr_diagonal)
anti_diagonals.add(curr_anti_diagonal)
state[row][col] = "Q"
# Move on to the next row with the updated board state
backtrack(row + 1, diagonals, anti_diagonals, cols, state)
# "Remove" the queen from the board since we have already
# explored all valid paths using the above function call
cols.remove(col)
diagonals.remove(curr_diagonal)
anti_diagonals.remove(curr_anti_diagonal)
state[row][col] = "."
ans = []
empty_board = [["."] * n for _ in range(n)]
backtrack(0, set(), set(), set(), empty_board)
return ans
- code
class Solution:
def solveNQueens(self, n):
def DFS(queens, xy_dif, xy_sum):
p = len(queens)
if p==n:
result.append(queens)
return None
for q in range(n):
if q not in queens and p-q not in xy_dif and p+q not in xy_sum:
DFS(queens+[q], xy_dif+[p-q], xy_sum+[p+q])
result = []
DFS([],[],[])
return [ ["."*i + "Q" + "."*(n-i-1) for i in sol] for sol in result]
whenever a location (x, y) is occupied, any other locations (p, q ) where p + q = = x + y or p - q = = x - y would be invalid. We can use this information to keep track of the indicators (xy_dif and xy_sum ) of the invalid positions and then call DFS recursively with valid positions only. At the end, we convert the result (a list of lists; each sublist is the indices of the queens) into the desire format.