leetcode questions: Bit

common tricks

x & (-x) to isolate/get the rightmost 1-bit

This operation reverts all bits of x except the rightmost 1-bit.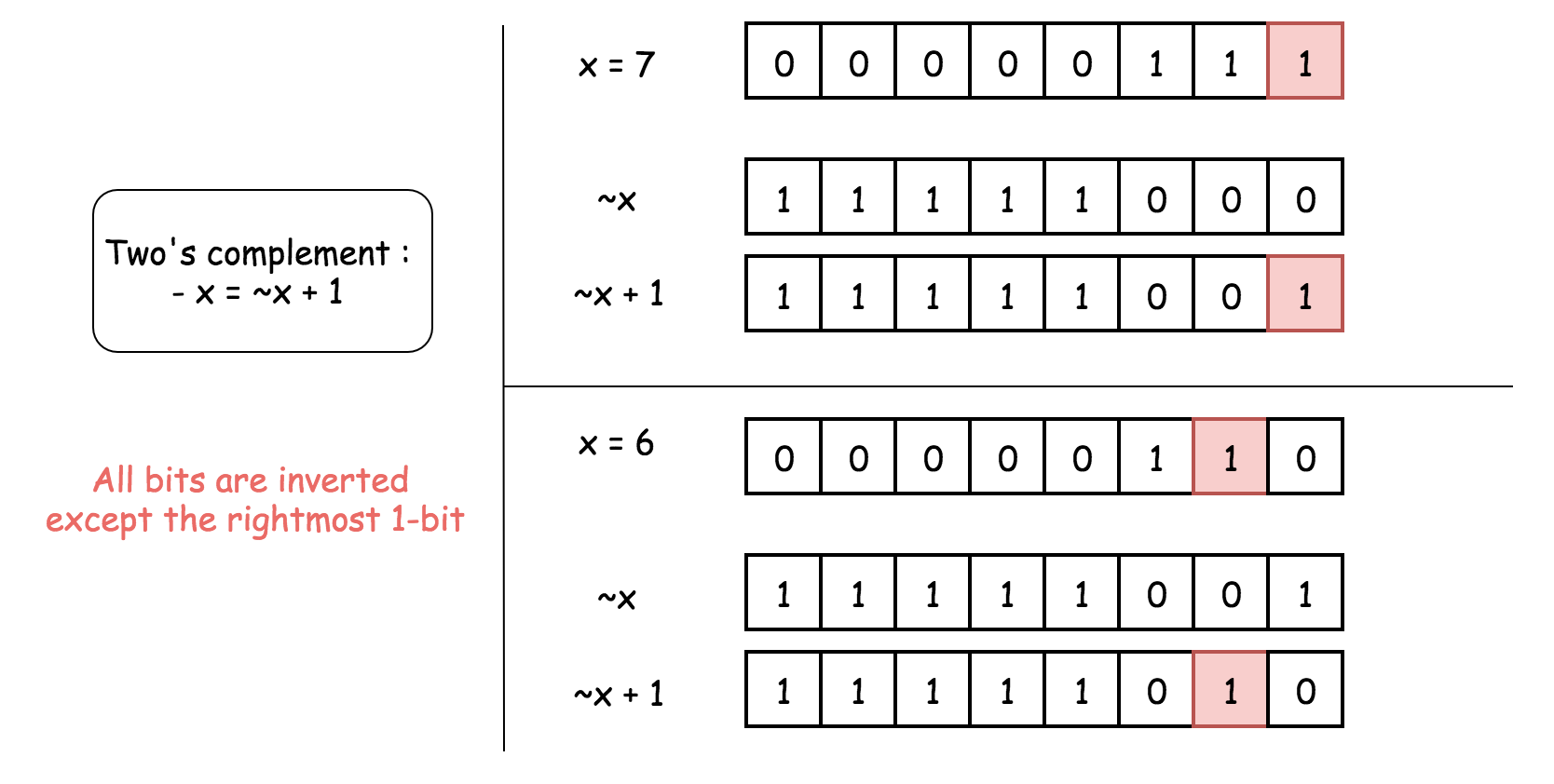

Hence, x and -x have just one bit in common - the rightmost 1-bit. That means that x & (-x) would keep that rightmost 1-bit and set all the other bits to 0.

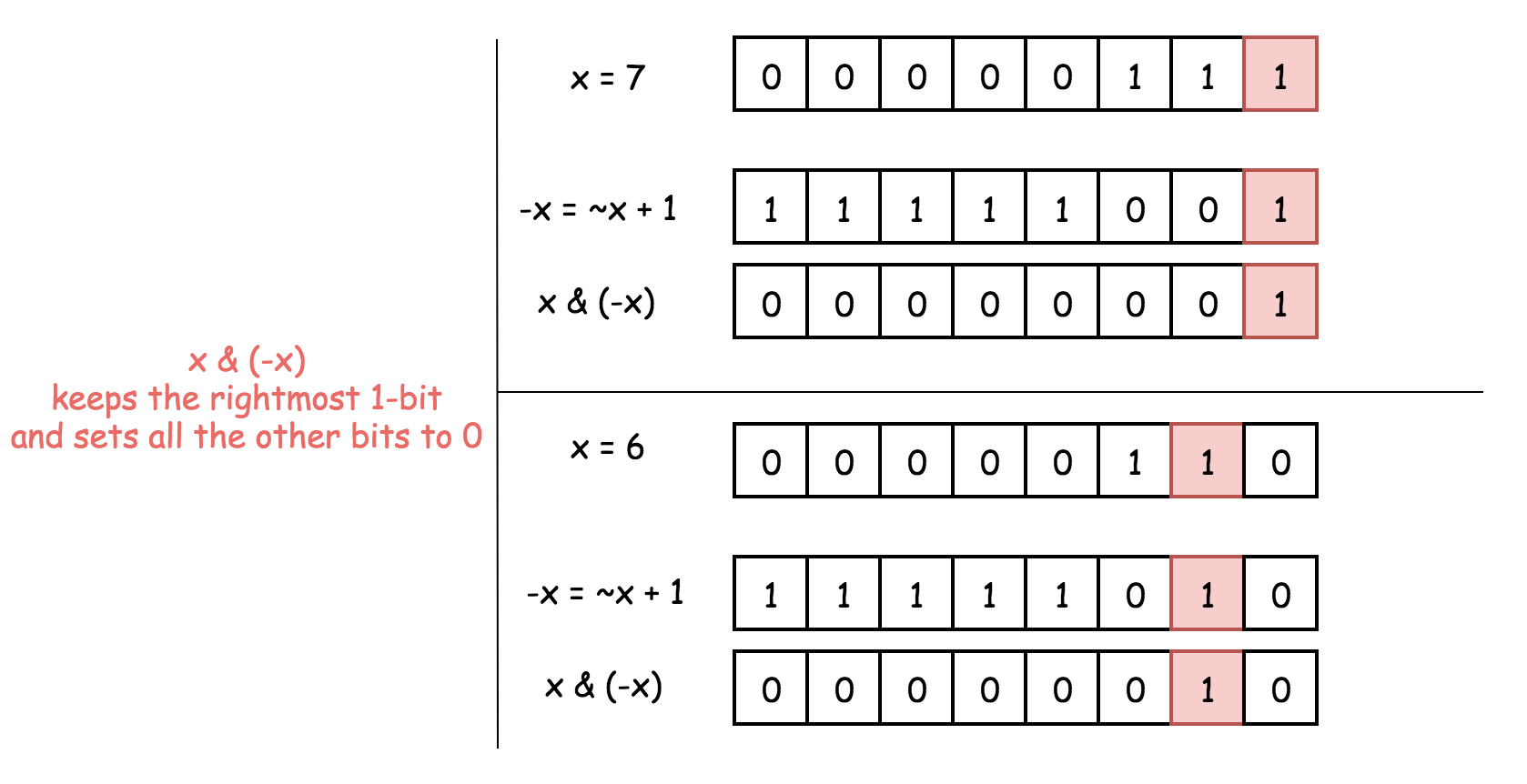
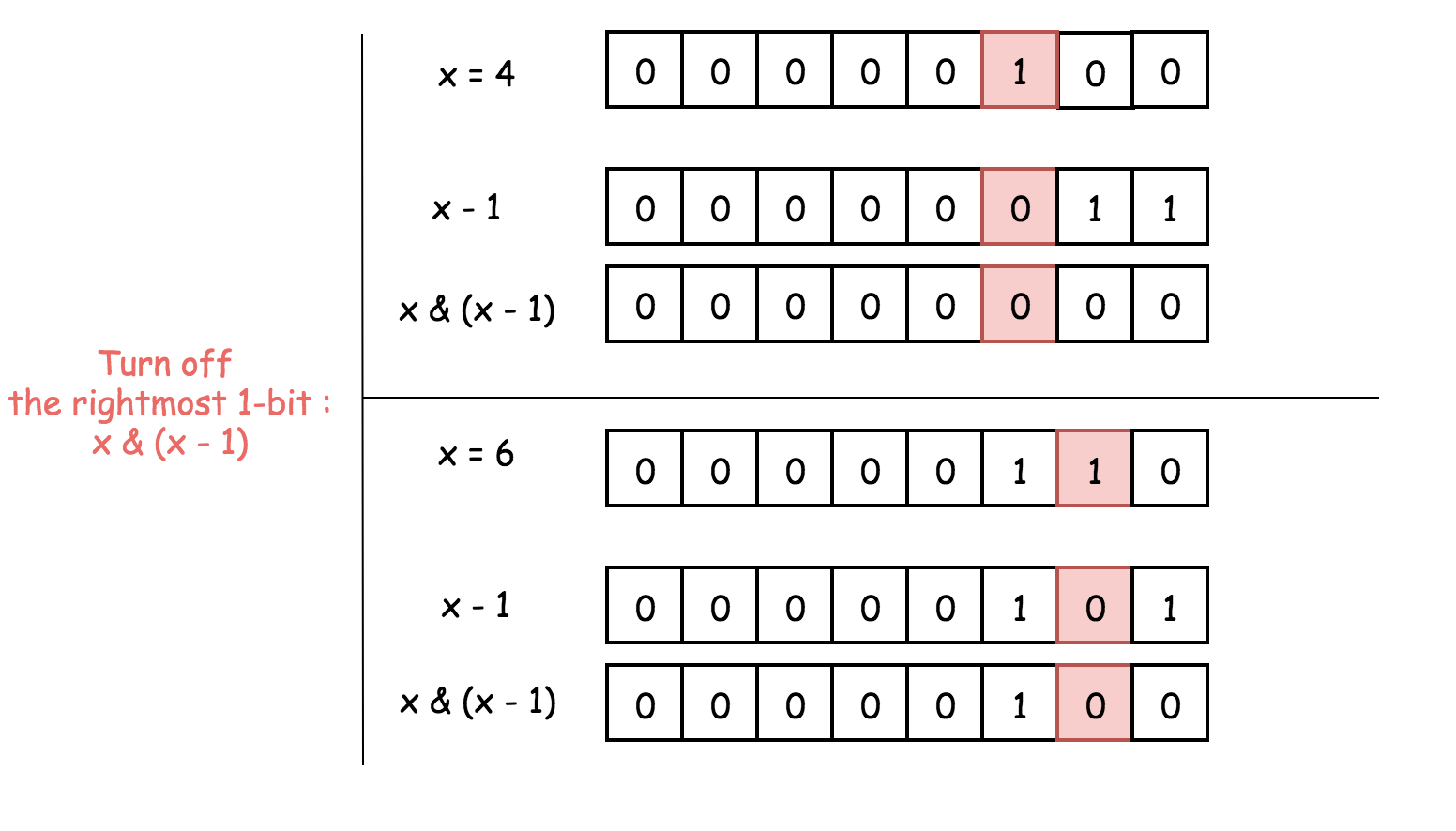
x & (x - 1) is a way to set the rightmost 1-bit to zero.

To subtract 1 means to change the rightmost 1-bit to 0 and to set all the lower bits to 1.

Now AND operator: the rightmost 1-bit will be turned off because 1 & 0 = 0, and all the lower bits as well.

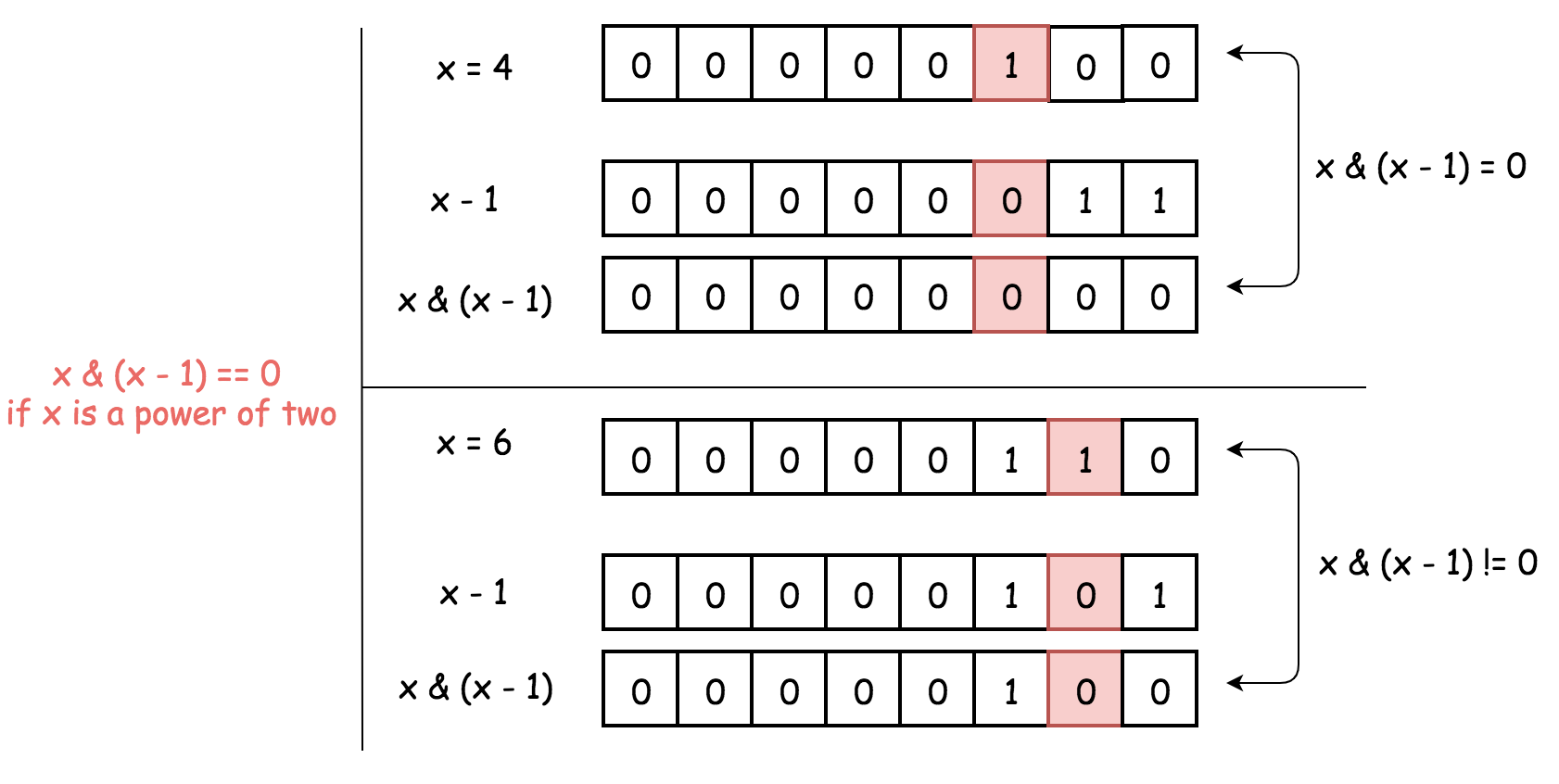
Detect Power of Two

The solution is straightforward: Power of two has just one 1-bit. x & (x - 1) sets this 1-bit to zero, and hence one has to verify if the result is zero x & (x - 1) == 0.

language specific

Python

• num.bit_length() find the first one

  • Code:

    class Solution:
        def findComplement(self, num):
            return ((1 << num.bit_length()) - 1) ^ num

• x*2^i = x<<i, 1000 << 1 = 2000

  • 5<<3 = 5*(2^3)

• def bin2dec(string_num):

  • return str(int(string_num, 2))

• num to bin string: bin(1234)[2:]

  • bin(4) -> 0b1000

Java

return Integer.bitCount(n); Number of 1 bits in integer n.

class Solution {
  public String addBinary(String a, String b) {
    return Integer.toBinaryString(Integer.parseInt(a, 2) + Integer.parseInt(b, 2));
  }
}

Integer.highestOneBit()

Code:

class Solution {
  public int findComplement(int num) {
    return (Integer.highestOneBit(num) << 1) - num - 1;
  }
}

questions

338. Counting Bits

Given an integer n, return **an array ans of length n + 1 such that for each **i__ (0 <= i <= n), ans[i] is the number of 1’s in the binary representation of __i.

Example 1: Input: n = 2 Output: [0,1,1] Explanation: 0 —> 0 1 —> 1 2 —> 10 Example 2: Input: n = 5 Output: [0,1,1,2,1,2] Explanation: 0 —> 0 1 —> 1 2 —> 10 3 —> 11 4 —> 100 5 —> 101

Constraints:

0 <= n <= 105

Code:

class Solution:
    def countBits(self, n: int) -> List[int]:
        res = [0] * (n + 1)
        for i in range(1, n + 1):
            res[i] = res[i & (i - 1)] + 1
        return res

67. Add Binary

Given two binary strings a and b, return their sum as a binary string.

Example 1: Input: a = “11”, b = “1” Output: “100”

Example 2: Input: a = “1010”, b = “1011” Output: “10101”

Constraints:

1 <= a.length, b.length <= 104
a and b consist only of '0' or '1' characters.
Each string does not contain leading zeros except for the zero itself.

Code:

class Solution:
    def addBinary(self, a, b) -> str:
        x, y = int(a, 2), int(b, 2)
        while y:
            x, y = x ^ y, (x & y) << 1
        return bin(x)[2:]

371. Sum of Two Integers

Given two integers a and b, return the sum of the two integers without using the operators + and -.

Example 1:

Input: a = 1, b = 2 Output: 3 Example 2:

Input: a = 2, b = 3 Output: 5

Constraints:-1000 <= a, b <= 1000

Code:

class Solution {
    public int getSum(int a, int b) {
        while (b != 0) {
            int answer = a ^ b;
            int carry = (a & b) << 1;
            a = answer;
            b = carry;
        }

        return a;
    }
}

Code:

class Solution:
    def getSum(self, a: int, b: int) -> int:

        mask = 0xffffffff

        while b & mask:
            _carry = a & b
            a = a ^ b
            b = _carry << 1

        # for overflow condition like
        # -1
        #  1
        return (a & mask) if b > mask else a

231. Power of Two

Given an integer n, return true if it is a power of two. Otherwise, return false. An integer n is a power of two, if there exists an integer x such that n == 2x.

Example 1: Input: n = 1 Output: true Explanation: 20 = 1 Example 2: Input: n = 16 Output: true Explanation: 24 = 16 Example 3: Input: n = 3 Output: false

Constraints:

-231 <= n <= 231 - 1

Code:

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        while n > 1:
            if n % 2 != 0: return False
            n = n // 2
        return n == 1

Code:

class Solution(object):
    def isPowerOfTwo(self, n):
        if n == 0:
            return False
        return n & (-n) == n

Code:

class Solution {
  public boolean isPowerOfTwo(int n) {
    if (n == 0) return false;
    long x = (long) n;
    return (x & (-x)) == x;
  }
}

476. Number Complement

The complement of an integer is the integer you get when you flip all the 0’s to 1’s and all the 1’s to 0’s in its binary representation.

For example, The integer 5 is “101” in binary and its complement is “010” which is the integer 2.Given an integer num, return its complement.

Example 1: Input: num = 5 Output: 2 Explanation: The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.

Example 2: Input: num = 1 Output: 0 Explanation: The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.

Constraints:

1 <= num < 231

Code:

class Solution:
    def findComplement(self, num):
        # bitmask has the same length as num and contains only ones 1...1
        bitmask = num
        bitmask |= (bitmask >> 1)
        bitmask |= (bitmask >> 2)
        bitmask |= (bitmask >> 4)
        bitmask |= (bitmask >> 8)
        bitmask |= (bitmask >> 16)
        # flip all bits
        return bitmask ^ num

Code:

class Solution:
    def findComplement(self, num: int) -> int:
        reverse = []
        num_bin = bin(num)
        for i in range(2, len(num_bin)):
            reverse.append(str(int(num_bin[i]) ^ 1))
        return int("".join(reverse), 2)

Code:

class Solution {
  public int findComplement(int num) {
    return (Integer.highestOneBit(num) << 1) - num - 1;
  }
}

Code:

class Solution:
    def findComplement(self, num):
        return ((1 << num.bit_length()) - 1 ) ^ num