Cheapest Flights Within K Stops - LeetCode
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei. You are also given three integers src, dst, and k, return __the cheapest price from src to dst with at most k stops. If there is no such route, return __-1.
Example 1:
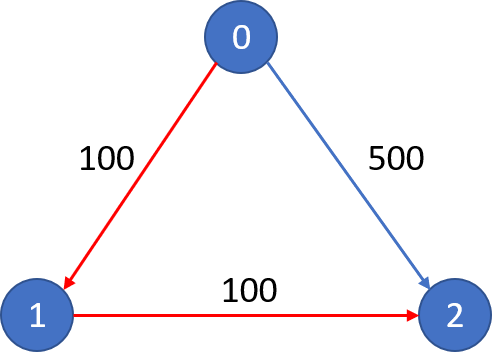
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown. The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture. Example 2:

Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown. The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.
Constraints:
1 <= n <= 100
0 <= flights.length <= (n * (n - 1) / 2)
flights[i].length == 3
0 <= fromi, toi < n
fromi != toi
1 <= pricei <= 104
There will not be any multiple flights between two cities.
0 <= src, dst, k < n
src != dst
- code #bellmanford
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
graph = defaultdict(list)
for start, end, cost in flights:
graph[end].append((start, cost))
pre = [inf] * n
pre[src] = 0
cur = pre[:]
for _ in range(k + 1):
for i in range(n):
for begin, cost in graph[i]:
cur[i] = min(cur[i], pre[begin] + cost)
if pre == cur: break
pre = cur[:]
return cur[dst] if cur[dst] != inf else -1
- code better, no need to build graph #bellmanford
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
pre = [inf] * n
pre[src] = 0
cur = pre[:]
for _ in range(k + 1):
for begin, end, cost in flights:
cur[end] = min(cur[end], pre[begin] + cost)
if pre == cur: break
pre = cur[:]
return cur[dst] if cur[dst] != inf else -1