Is Graph Bipartite? - LeetCode
There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:
There are no self-edges (graph[u] does not contain u).
There are no parallel edges (graph[u] does not contain duplicate values).
If v is in graph[u], then u is in graph[v] (the graph is undirected).
The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.
Return true__ if and only if it is bipartite__.
Example 1:
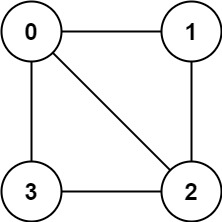Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]] Output: false Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.
Example 2:
Input: graph = [[1,3],[0,2],[1,3],[0,2]] Output: true Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.
Constraints:
graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u] does not contain u.
All the values of graph[u] are unique.
If graph[u] contains v, then graph[v] contains u.
- code
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
setA = set()
setB = set()
visited = set()
for node in range(len(graph)):
if node not in visited:
q = deque([(node, setA)])
visited.add(node)
setA.add(node)
while q:
cur, curGroup = q.popleft()
for nei in graph[cur]:
if nei in curGroup: return False
if curGroup == setB and nei not in setA:
setA.add(nei)
visited.add(nei)
q.append((nei, setA))
elif curGroup == setA and nei not in setB:
setB.add(nei)
visited.add(nei)
q.append((nei, setB))
return True