https://leetcode.com/problems/range-sum-query-2d-immutable/
Given a 2D matrix matrix, handle multiple queries of the following type:
Calculate the **sum** of the elements of matrix inside the rectangle defined by its **upper left corner** (row1, col1) and **lower right corner** (row2, col2).Implement the NumMatrix class:
NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the **sum** of the elements of matrix inside the rectangle defined by its **upper left corner** (row1, col1) and **lower right corner** (row2, col2).
Example 1:
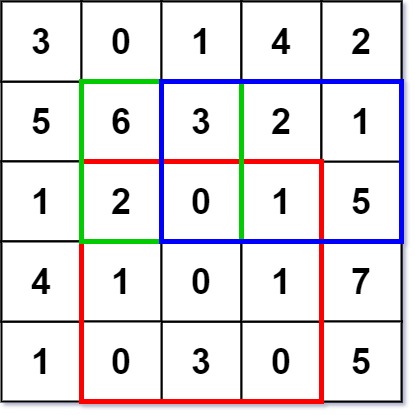Input [“NumMatrix”, “sumRegion”, “sumRegion”, “sumRegion”] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]] Output [null, 8, 11, 12] Explanation NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]); numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle) numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle) numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
Constraints:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-105 <= matrix[i][j] <= 105
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 104 calls will be made to sumRegion.
- code
class NumMatrix {
private int[][] dp;
public NumMatrix(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) return;
dp = new int[matrix.length][matrix[0].length + 1];
for (int r = 0; r < matrix.length; r++) {
for (int c = 0; c < matrix[0].length; c++) {
dp[r][c + 1] = dp[r][c] + matrix[r][c];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sum = 0;
for (int row = row1; row <= row2; row++) {
sum += dp[row][col2 + 1] - dp[row][col1];
}
return sum;j
}
}
- code
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
m, n = len(matrix), len(matrix[0])
self.dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(m):
for j in range(n):
self.dp[i+1][j+1] = self.dp[i][j+1] + self.dp[i+1][j] + matrix[i][j] - self.dp[i][j]
def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
return self.dp[row2+1][col2+1] - self.dp[row1][col2+1] - self.dp[row2+1][col1] + self.dp[row1][col1]