According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.” The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
Any live cell with fewer than two live neighbors dies as if caused by under-population.
Any live cell with two or three live neighbors lives on to the next generation.
Any live cell with more than three live neighbors dies, as if by over-population.
Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return __the next state__.
Example 1:
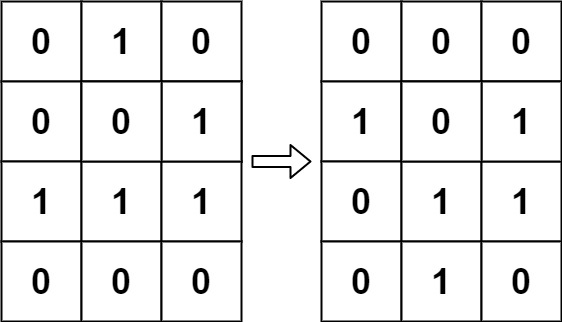Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]] Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
Example 2:
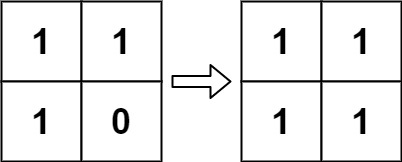Input: board = [[1,1],[1,0]] Output: [[1,1],[1,1]]
Constraints:
m == board.length
n == board[i].length
1 <= m, n <= 25
board[i][j] is 0 or 1.
- code
class Solution {
public void gameOfLife(int[][] board) {
int[] neighbors = {0, 1, -1};
int rows = board.length;
int cols = board[0].length;
for (int row = 0; row < rows; row++){
for (int col = 0; col < cols; col++){
// count nei
int liveNei = 0;
for (int dx: neighbors){
for (int dy: neighbors){
if (!(dx == 0 && dy == 0)){
int nx = row + dx;
int ny = col + dy;
if ((nx >= 0 && nx < rows) && (ny >= 0 && ny < cols) && Math.abs(board[nx][ny]) == 1){
liveNei++;
}
}
}
}
// mark
if (liveNei == 3 && board[row][col] == 0) board[row][col] = 2;
else if ((liveNei > 3 || liveNei < 2) && board[row][col] == 1) board[row][col] = -1;
}
}
// Get the final representation for the newly updated board.
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
if (board[row][col] > 0) {
board[row][col] = 1;
} else {
board[row][col] = 0;
}
}
}
}
}
- code
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
m, n = len(board), len(board[0])
copyb = copy.deepcopy(board)
def countLive(x, y):
count_live = 0
for dx, dy in [(-1,-1),(-1,0),(-1,1),(0,1),(1,1),(1,0),(1,-1),(0,-1)]:
nx, ny = x + dx, y + dy
if 0 <= nx < m and 0 <= ny < n and copyb[nx][ny] == 1:
count_live += 1
return count_live
for i in range(m):
for j in range(n):
ctLive = countLive(i, j)
if copyb[i][j] and ctLive in (2,3): board[i][j] = 1
elif copyb[i][j] == 0 and ctLive == 3: board[i][j] = 1
else: board[i][j] = 0
- code
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
neighbors = [(1,0), (1,-1), (0,-1), (-1,-1), (-1,0), (-1,1), (0,1), (1,1)]
rows = len(board)
cols = len(board[0])
# Iterate through board cell by cell.
for row in range(rows):
for col in range(cols):
live_neighbors = 0
for dx, dy in neighbors:
r, c = row + dx, col + dy
# Check the validity of the neighboring cell and if it was originally a live cell.
if 0 <= r < rows and 0 <= c < cols and abs(board[r][c]) == 1:
live_neighbors += 1
# Rule 1 or Rule 3
if board[row][col] == 1 and (live_neighbors < 2 or live_neighbors > 3):
# -1 signifies the cell is now dead but originally was live.
board[row][col] = -1
# Rule 4
if board[row][col] == 0 and live_neighbors == 3:
# 2 signifies the cell is now live but was originally dead.
board[row][col] = 2
# Get the final representation for the newly updated board.
for row in range(rows):
for col in range(cols):
if board[row][col] > 0:
board[row][col] = 1
else:
board[row][col] = 0