Graph Valid Tree - LeetCode You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph. Return true if the edges of the given graph make up a valid tree, and false otherwise.
Example 1:
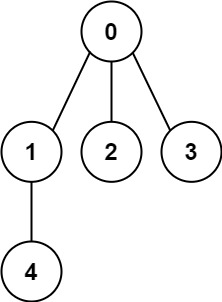
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]] Output: true Example 2:
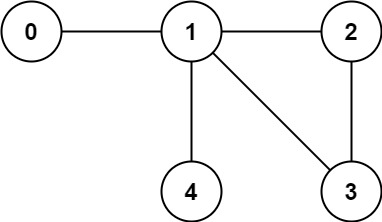
Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]] Output: false C:
- code dfs
class Solution:
def validTree(self, n: int, edges: List[List[int]]) -> bool:
if len(edges) != n - 1: return False
# Create an adjacency list.
adj_list = [[] for _ in range(n)]
for A, B in edges:
adj_list[A].append(B)
adj_list[B].append(A)
# We still need a seen set to prevent our code from infinite
# looping if there *is* cycles (and on the trivial cycles!)
seen = {0}
stack = [0]
while stack:
node = stack.pop()
for neighbour in adj_list[node]:
if neighbour in seen:
continue
seen.add(neighbour)
stack.append(neighbour)
return len(seen) == n
- code dsu
class Solution:
def validTree(self, n: int, edges: List[List[int]]) -> bool:
if len(edges) != n-1: return False
root = [i for i in range(n)]
rank = [1] * n
def find(i):
if i == root[i]:
return i
root[i] = find(root[i])
return root[i]
def union(i, j):
rti = find(i)
rtj = find(j)
if rti == rtj:
return False # cycle found
if rank[rti] < rank[rtj]:
root[rti] = rtj
elif rank[rti] > rank[rtj]:
root[rtj] = rti
else:
root[rtj] = rti
rank[rti] += 1
return True
for i,j in edges:
if not union(i, j):
return False
return True