Path With Minimum Effort - LeetCode
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort. A route’s effort is the maximum absolute difference in heights between two consecutive cells of the route. Return the minimum effort required to travel from the top-left cell to the bottom-right cell.
Example 1:
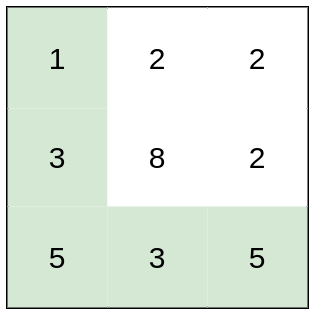Input: heights = [[1,2,2],[3,8,2],[5,3,5]] Output: 2 Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells. This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
Example 2:
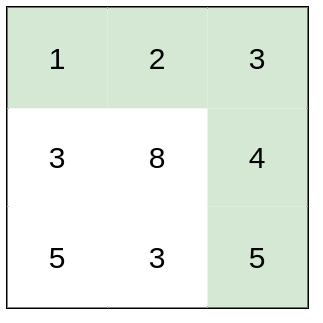Input: heights = [[1,2,3],[3,8,4],[5,3,5]] Output: 1 Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
Example 3:
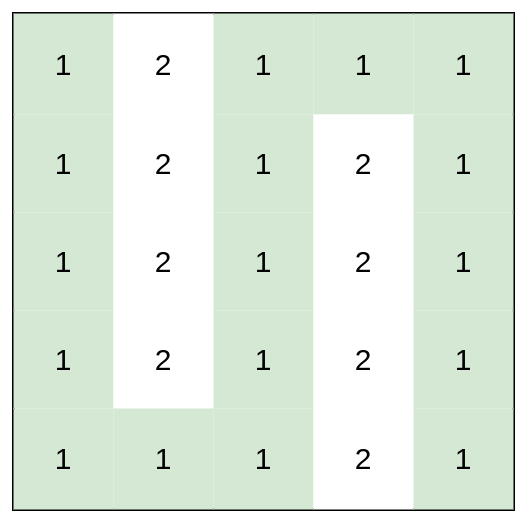Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]] Output: 0 Explanation: This route does not require any effort.
Constraints:
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106
- code TLE DP usually only works with directional matrix, one way or two, for this problem 4 directions are valid.
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
direction = [[-1, 0], [1, 0], [0, 1], [0, -1]]
m = len(heights)
n = len(heights[0])
dis = [[inf for _ in range(n)] for _ in range(m)]
dis[0][0] = 0
pre = copy.deepcopy(dis)
for round in range(m * n):
for i in range(m):
for j in range(n):
for dx, dy in direction:
nei_x, nei_y = i + dx, j + dy
if 0 <= nei_x < m and 0 <= nei_y < n:
dis[i][j] = min(dis[i][j], max(abs(heights[i][j] - heights[nei_x][nei_y]), dis[nei_x][nei_y]))
if pre == dis: break
pre = copy.deepcopy(dis)
return dis[-1][-1]
- code TLE Dijkstra, the missing point: before pushing neighbour nodes, check if the new diff[nx][ny] is smaller,
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
m, n = len(heights), len(heights[0])
diff = [[inf for _ in range(n)] for _ in range(m)]
diff[0][0] = 0
q = [[0, (0,0)]] # max diff, point
direction = [[-1,0],[1,0],[0,1],[0,-1]]
visited = set()
while q:
cur_diff, cur = heapq.heappop(q)
if cur_diff >= diff[-1][-1]: break
visited.add(cur)
x, y = cur
for dx, dy in direction:
nx, ny = x + dx, y + dy
if 0 <= nx < m and 0 <= ny < n and (nx, ny) not in visited:
diff[nx][ny] = min(diff[nx][ny], max(abs(heights[nx][ny] - heights[x][y]), cur_diff))
heapq.heappush(q, [diff[nx][ny], (nx, ny)])
return diff[-1][-1]
- code #Dijkstra as long as a new edge won’t decrease the path, i.e. diff won’t decrease, we can potentially use Dijkstra(no negative edges)
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
m, n = len(heights), len(heights[0])
diff = [[inf] * n for _ in range(m)]
diff[0][0] = 0
q = [[0, 0, 0]] # max diff, (x, y)
direction = [[-1,0],[1,0],[0,1],[0,-1]]
visited = [[False] * n for _ in range(m)]
while q:
cur_diff, x, y = heapq.heappop(q)
visited[x][y] = True
for dx, dy in direction:
nx, ny = x + dx, y + dy
if 0 <= nx < m and 0 <= ny < n and not visited[nx][ny]:
newdiff = min(diff[nx][ny], max(abs(heights[nx][ny] - heights[x][y]), cur_diff))
if newdiff < diff[nx][ny]:
diff[nx][ny] = newdiff
heapq.heappush(q, [diff[nx][ny], nx, ny])
return diff[-1][-1]
- code #unionfind sort all edges and start to merge, as long as source and end has the same root.
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
class UnionFind:
def __init__(self, size):
self.parent = [x for x in range(size)]
self.rank = [0]*(size)
def find(self, i):
if self.parent[i] != i:
self.parent[i] = self.find(self.parent[i])
return self.parent[i]
def union(self, x, y):
parent_x = self.find(x)
parent_y = self.find(y)
if parent_x != parent_y:
if self.rank[parent_x] > self.rank[parent_y]:
self.parent[parent_y] = parent_x
elif self.rank[parent_x] < self.rank[parent_y]:
self.parent[parent_x] = parent_y
else:
self.parent[parent_y] = parent_x
self.rank[parent_x] += 1
row = len(heights)
col = len(heights[0])
if row == 1 and col == 1:
return 0
edge_list = []
for current_row in range(row):
for current_col in range(col):
if current_row > 0:
difference = abs(
heights[current_row][current_col] -
heights[current_row - 1][current_col])
edge_list.append(
(difference, current_row * col + current_col,
(current_row - 1) * col + current_col))
if current_col > 0:
difference = abs(
heights[current_row][current_col] -
heights[current_row][current_col - 1])
edge_list.append(
(difference, current_row * col + current_col, current_row
* col + current_col - 1))
edge_list.sort()
union_find = UnionFind(row*col)
for difference, x, y in edge_list:
union_find.union(x, y)
if union_find.find(0) == union_find.find(row*col-1):
return difference
return -1
- code BFS + binary search
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
row = len(heights)
col = len(heights[0])
def canReachDestinaton(x, y, mid):
if x == row-1 and y == col-1:
return True
visited[x][y] = True
for dx, dy in [[0, 1], [1, 0], [0, -1], [-1, 0]]:
adjacent_x = x + dx
adjacent_y = y + dy
if 0 <= adjacent_x < row and 0 <= adjacent_y < col and not visited[
adjacent_x][adjacent_y]:
current_difference = abs(
heights[adjacent_x][adjacent_y]-heights[x][y])
if current_difference <= mid:
visited[adjacent_x][adjacent_y] = True
if canReachDestinaton(adjacent_x, adjacent_y, mid):
return True
left = 0
right = 10000000
while left < right:
mid = (left + right)//2
visited = [[False]*col for _ in range(row)]
if canReachDestinaton(0, 0, mid):
right = mid
else:
left = mid + 1
return left
The real reason why the binary search approach works with BFS or DFS is that by defining a diff limit, the search space dramatically decreased, because we don’t need BFS/DFS to exhaust all the paths to the target anymore, we just need to find ONE path that satisfy the diff limit. Thus, if we find ourself at a Cell that satisfies a diff limit, we don’t care about other paths that get to this Cell anymore, that’s why we can use “visited” to eliminate paths exploration. Without a diff limit, we can no longer use this naive “visited” way of tracking and the search space becomes 3^(M*N) as we’d have to exhaust all the paths to find the one with min diff. -billmaxwell on leetcode https://leetcode.com/problems/path-with-minimum-effort/solution/977158