Path With Maximum Minimum Value - LeetCode
Given an m x n integer matrix grid, return __the maximum score of a path starting at (0, 0) and ending at __(m - 1, n - 1) moving in the 4 cardinal directions. The score of a path is the minimum value in that path.
For example, the score of the path 8 → 4 → 5 → 9 is 4.
Example 1:
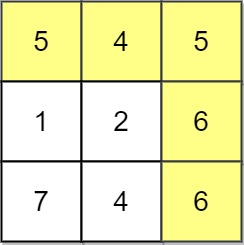 Input: grid = [[5,4,5],[1,2,6],[7,4,6]] Output: 4 Explanation: The path with the maximum score is highlighted in yellow.
Example 2:
Input: grid = [[5,4,5],[1,2,6],[7,4,6]] Output: 4 Explanation: The path with the maximum score is highlighted in yellow.
Example 2:
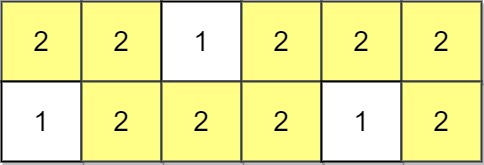 Input: grid = [[2,2,1,2,2,2],[1,2,2,2,1,2]] Output: 2
Example 3:
Input: grid = [[2,2,1,2,2,2],[1,2,2,2,1,2]] Output: 2
Example 3:
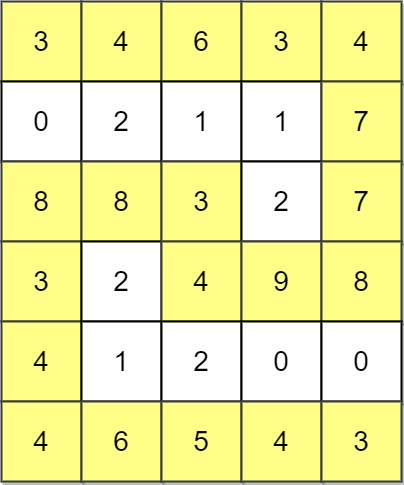 Input: grid = [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]] Output: 3
Input: grid = [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]] Output: 3
Constraints:
m == grid.length
n == grid[i].length
1 <= m, n <= 100
0 <= grid[i][j] <= 109
- code
class Solution:
def maximumMinimumPath(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]
def dfs(i, j, mini, visited):
if i == m - 1 and j == n - 1:
return True
for dx, dy in directions:
nx, ny = i + dx, j + dy
if 0 <= nx < m and 0 <= ny < n and (nx, ny) not in visited:
if grid[nx][ny] >= mini:
visited.add((nx, ny))
if dfs(nx, ny, mini, visited): return True
return False
res = 0
start, end = 0, min(grid[0][0], grid[-1][-1]) + 1 # left open, right closed so plus one
while start < end:
mid = (start + end) // 2
visited = set()
visited.add((0, 0))
if dfs(0, 0, mid, visited):
start = mid + 1 # current is working, move to one step right
else:
end = mid
return end - 1 # or start - 1