Data analysis module outline

warwick

For Warwick University module 910, Data analysis.

2. math back ground

  • why frequency/rank for heavy tailed?

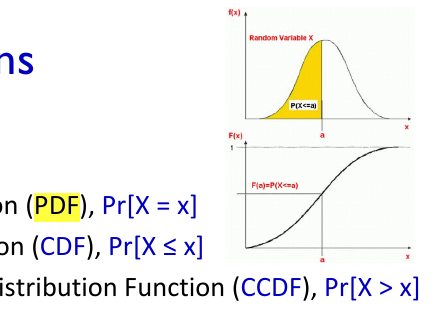
The frequency/rank plot because the CCDF is a monotonous function. Moreover, unlike the PDF function, the CCDF displays a significantly lower variability in the tail.

  • independence: event and random variables
    • HH and TT
      • not independent because the mere occurrence of one would tell us for sure that the other can’t happen.
  • Conditional Probability
  • Heavy-Tailed Distributions roughly non-negligible probabilities at large values far to the right.
    • CDF+CCDF=1
    • Real Histograms
    • log-log plot is also a great trick to visualize data spanning a wide range of data.
    • Pareto Distribution
    • Good (Enough) Method: Frequency/Rank Plot the sharp drop in variance in the tail is the fact hat the CCDF is a monotonous function
    • the Q-Q curve is non-decreasing

3. statistics

  • quantile-quantile plot
    • Allows comparison of attributes of different cardinality
    • Plot points corresponding to f-quantile of each attribute
    • If close to line y=x, evidence for same distribution
  • PMCC = (E(XY)-EXEY)/($\sigma x \sigma y$) = cov(xy)/($\sigma x \sigma y$)
    • pmcc between -1,1
    • Measures linear dependence in terms of simple quantities

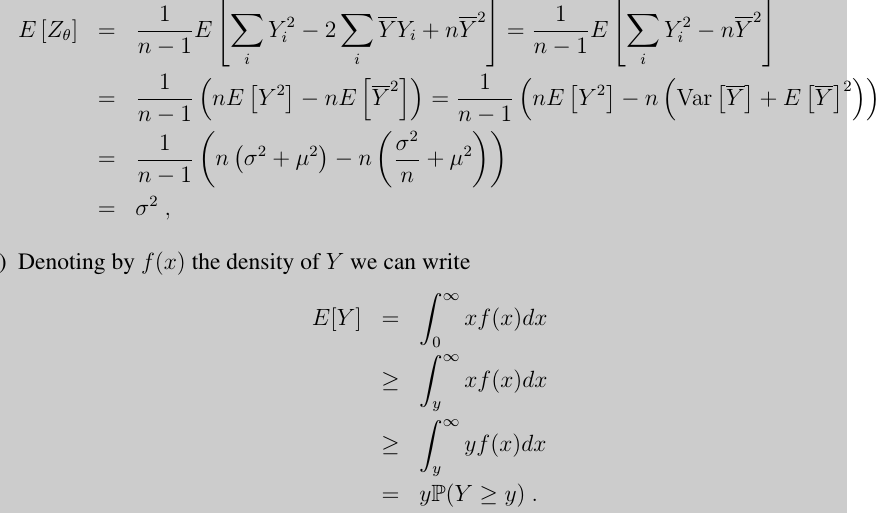
20190526115240.png 1-w2{10} 20190522113900.png-w10 > table, correlated. < table, no correlation. 20190524145041.png 20190526111808.png

3.1 handle problems

  1. numeric data, ranges vastly different
  • range scaling, to 0,1.
  • statistical scaling, (x-u)/a
  1. ordered data: replace each point with its position in the ordering
  2. mixed data: encode each dimension into the range 0,1. use Lp distance 20190526120355.png
  3. handle missing values
  • drop the whole record
  • fill in missing values manually
  • as unknown, ensure can handle
  • no ideal solution
  1. Noise, hard to tell. statistical tests
  2. Outliers: extreme values
  • finding in numerica data
    • sanity check, mean ,max, std dev
    • visual, plot , far from rest
    • rule based, set limits
    • data based, declare if > 6
  • categoric data
    • visual, look at frequency statistics, low frequency

dealing outliers: delete, clip(change to max/min), treat as missing

  1. discretization: features have too many values
  • binning, place data into bands
  • use existing hierarchies in data
  1. random sampleing, stratifies, take samples from subsets
  2. feature selection
  • principal components analysis
  • greedy attribute selection

4.regression

  • regression 4
    • Assuming unbiased independent noise with bounded variance
    • PMCC , Product-Moment Correlation Coefficient determines the quality of the linear regression between X and Y
    • R2 = Cov2(X,Y) /(Var(X)Var(Y)) = PMCC^2
      • measure the coefficient of determination, how much the model explains the variance in Y
      • 1, good fit, 0 ,weak fit to the model
    • Two perfectly correlated attributes can’t be used in regression
      • Violates requirement of no linearly dependent columns
      • Regularization can fix this: ensures matrix is non-singular

  • dealing with categoric attributes

    • numerically encode categoric explanatory variables
    • simple case: 0/1, include this new variable in the regression
    • general categoric attributes, create a binary variable for each possibility

  • Regularization in regression: To handle the danger of overfitting the model of the data, include the parameters in the optimization

6. classification

  • measures

    • precision : tp/(tp+fp)
    • recall: tp/(tp+fn)
    • F1 2precision*recall/(precision+recall)
    • ROC: recall-y, fp-x(fp/(fp+tn))

  • k-fold cross validation

    • Divide data into k equal pieces (folds)
    • use k-1 for training, evaluate accuracy on 1 fold, repeat

  • Entropy H= -plog(p),

    • information gain=H-Hsplit
    • gain ratio = (Hx-Hsplit)/Hsplit

  • kappa

    • higher is better
    • compares accuracy to random guessing
    • Po as the observed agreement between two labelers
    • Pe is the agreement if both are labeling at random
    • K = (Po-Pe)/(1-Pe)

  • pruning

    • prepruning:add additional stopping conditions when building
    • Postpruning: build full tree, then decide which branches to prune

  • SVM

    • assume data is linearly separable
    • seeks the plane that maximizes the margin between the classes 20190524141939.png

7. clustering

  • k-center Furthest point for minimize the max distance between pairs in same cluster
    • 2-approximation
      • asuume the furthest point to all center>2opt
      • then the distances between all centers are also>2opt
      • we have k+1 points with distances>2opt between every pair
      • since each point has a center with distance < opt
      • there exists a pair of points with same center, the distance is at most 2opt
      • contradiction!
  • k-medians minimize the average distance from each point to its closest centre
  • k means Lloyd minimize the sum of squared distance
    • assign each point to its cloest center
    • compute new centroid of each cluster, until no change
  • Hierarchical agglomerative HAC
    • merge closest pair of clusters
    • single, complete, average link
      • single: d(C1,C2) = min d(c1 in C1, c2 in C2)
      • complete: d(C1,C2) = max d(c1 in C1, c2 in C2) max nodes between each cluster, then find the min
      • avg
    • Dc-Tc >= Db - Tb
    • 20190526164106.png
  • DBSCAN based on local density of data points
    • Epsilon, the radius to search for neighbours
    • MinPts, min start points to make one cluster
    • density reachable .->.
    • density connected .<-.->.

8. recommendation

  • recommendation 8
    • neighbourhood-based collaborative filtering
    • item-based collaborative filtering
    • matrix factoraization-singular value decomposition
      • solving the optimization
        • gradient descent
        • least squares
      • adding biases

9. social network analysis

  • social networks 9

    • concept
      • in-degree, out degree.
      • distance
      • diameter
    • link prediction on graphs
      • simplest: common neighbours will link
      • weighting common neighbours
    • finding important nodes
      • graph centrality
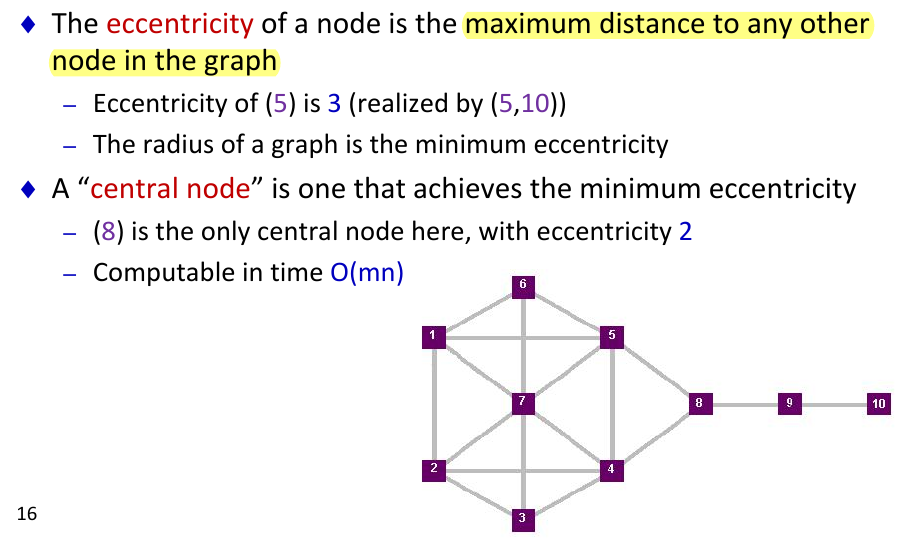
        • eccentrality
        • betweenness centrality
        • 20190526170755.png
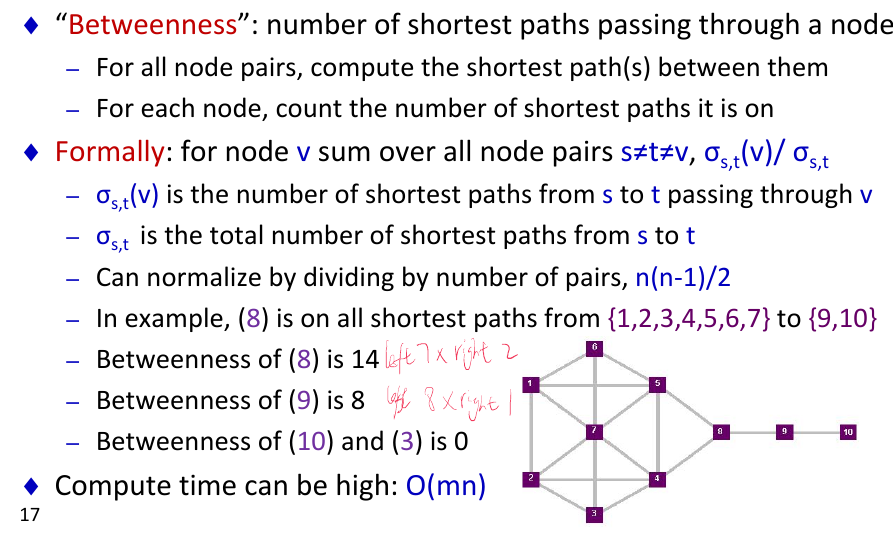
        • 20190526170845.png
    • pageRank
      • eigenvector formulation
        • r=Mr
      • power iteration method
      • random walk interpretation
    • classification in social networks

  • clustering coefficient

    • measures the fraction of triangles
    • (number of triangles)/(number of pairs of common neighbours)

page-rank

here (1,2)(1,3)

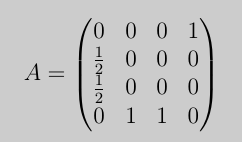
  • key shortcoming of simplified version?

The problem is the periodic behavior, meaning that PageRank cannot identify the most important web-page. One solution is to create a self-loop (e.g., (1, 1)), in which case the iterative procedure from (a) would be guaranteed to converge.

  • main objective? how achieved?

PageRank computes the importance of web-pages. This is achieved by leveraging the transition matrix.